Causal Reinforcement Learning: A Primer

As part of any honours degree at the University of Cape Town, one is obliged to write a thesis droning on about some topic. Luckily for me, applied mathematics can pertain to pretty much anything of interest. Lo and behold, my thesis on merging causality and reinforcement learning - two subject I have made some fuss about on this blog before. This was entitled Climbing the Ladder: A Survey of Counterfactual Methods in Decision Making Processes and was supervised by Dr Jonathan Shock.

In this series of posts I will break down my thesis into digestible blog chucks and go into quite some detail of the emerging field of Causal Reinforcement Learning (CRL) - which is being spearheaded by Elias Bareinboim and Judea Pearl, among others. I will try to present this in such a way as to satisfy those craving some mathematical detail whilst also trying to paint a broader picture as to why this is generally useful and important. Each of these blog posts will be self contained in some way. Perhaps it will be about a specific idea or research paper. In this case, it is just a primer for what is to come. Let’s begin!

This Series

1. Causal Reinforcement Learning: A Primer
2. Preliminaries for CRL
3. Task 1: Generalised Policy Learning
4. Task 2: Interventions: Where and When?
5. Task 3: Counterfactual Decision Making
6. Task 4: Generalisability and Robustness
7. Task 5: Learning Causal Models
8. Task 6: Causal Imitation Learning
9. Wrapping Up: Where To From Here?

So what’s this all about?

All reasonings concerning matter of fact seem to be founded on the relation of cause and effect. By means of that relation alone we can go beyond the evidence of our memory and senses. - David Hume [1].

In an earlier blog post I mentioned that R.A. Fisher, one of the fathers of modern statistics, was stringently opposed to causal conclusions without overwhelming evidence. See, for example, the debate on whether smoking causes cancer (e.g. [2], [3], [4]). The anachronism, correlation does not imply causation, was (and is) responsible for so much misguided science. If anything, it seems to imply that we can never state that \(A\) causes \(B\) by analysis of data alone. But is statistics really powerless when faced with the battle of determining causation?

Recently there has been much interest in the techniques developed to infer causation from data, especially with the proliferation of statistical learning techniques in the fields of deep learning, for example. Graphical techniques employing DAGs have been especially popular in recent years, often locking horns with those in favour of the Neyman–Rubin causal model [5] and potential outcomes framework (e.g. [6]). Regardless, anyone familiar with the works of Judea Pearl, such as his popular science book The Book of Why [7], is likely a passionate believer in the causal revolution.

With the rise in popularity of unsupervised methods in both machine learning and reinforcement learning paradigms, there is little doubt that inferring causal structure will play a crucial role in getting artificial agents to make informed decisions, especially in an uncertain world. Reinforcement learning agents are concerned with maximising cumulative reward over a long time horizon by following a sequence of optimal actions. Ensuring such an agent maintains a causal model for the world it operates in will undoubtedly make for interpretable models in a field otherwise filled with ’black-boxes’.

One should be careful not to confuse world models in model-based RL with a causal model. A causal model explicitly models the nature of the relationships of the underlying data generating process, whereas a RL world model attempts to simulate the predictive outputs due to an agent intervention. Causal and graphical models also extend the applicability of current decision making methods, most of which are only applicable under a narrow set of assumptions. Consider that reinforcement learning under an MDP formulation explicitly requires Markov processes. As we will discuss, this fails to account for some fundamental decision processes in the real world - including dynamic treatment regimes in the field of personalised medicine.

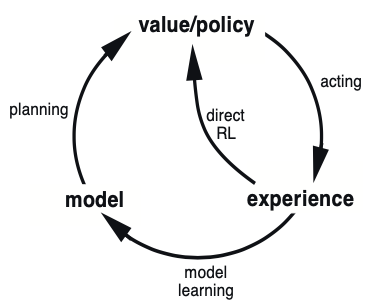
One can easily imagine how a generally intelligent agent would require long-term, non-Markov planning ability. Before continuing to develop the notions of causality, it should be made clear that we are working within the ladder of causation proposed by Judea Pearl [8]. In this framework there are three rungs on the causal hierarchy, each adding additional information not available to models belonging to a lower rung. These are (1) observational information, (2) interventional information, and (3) counterfactual information, with each building upon and subsuming the last.

Reinforcement learning naturally falls on the interventional rung since agents learn about optimal actions by observing outcomes due to their interventions in the system. They cannot, however, use interventional data to answer counterfactual - “what if?” - style questions without additional information. This is critical to acknowledge for much of the theory that follows.

The astute reader will point out that counterfactual quantities are inherently non-scientific because they cannot be proved to be true - what has happened, has happened. We do not claim otherwise. Rather, counterfactual quantities are useful for decision making - as is clear with any thought about how we reason in our daily lives. These blog posts will introduce the mathematical notion of causality from the perspective of statistics, and place it in the context of machine learning and artificial intelligence. Specifically, focus will be placed on developing and discussing the theory of causal reinforcement learning (CRL) so that an interested reader is prepared for dealing with state-of-the-art research and results. The six tasks introduced by Bareinboim [9] will be discussed through the surveying of relevant and recent literature. Finally the state of causal reinforcement will be discussed in the context of the current machine learning landscape and the quest for artificial general intelligence (AGI).

Ultimately, it comes down to this: RL is concerned with maximisation of cumulative reward over long time horizons while causal inference provides a set of tools and techniques to combine structural information about the data generating process, and data itself, to reason and infer up to a counterfactual nature - what would have happened had something been different? By adding causal structural information to sample efficient RL techniques we can boost learning performance in many domains. This combination of theory from different fields has led to successes in various domains.

References

• Header Image
• [1] David Hume.An enquiry concerning human understanding.Hackett, 2 edition, 1993.
• [2] Ronald A. Fisher. Cancer and smoking.Nature, 182:596–596, 1958.
• [3] Sir Ronald A. Fisher. Smoking: The cancer controversy. 1960.
• [4] L. Penrose. Cancer and smoking.Nature, 182:1178–1178, 1958.
• [5] D. Rubin. Causal inference using potential outcomes.Journal of the American Statistical Association,100:322 – 331, 2005.
• [6] Andrew Gelman et al. Resolving disputes between j. pearl and d. rubin on causal inference. https://statmodeling.stat.columbia.edu/2009/07/05/disputes_about/, 2009.
• [7] Judea Pearl and Dana Mackenzie.The Book of Why. Basic Books, New York, 2018.
• [8] Elias Bareinboim, Juan D. Correa, Duligur Ibeling, and Thomas Icard. On pearl’s hierarchy andthefoundations of causalinference. unpublished, 2020.
• [9] Elias Bareinboim. Causal reinforcement learning. ICML 2020, 2020.