One of the inherent problems an agent faces in some arbitrary environment is how to decide whether to explore and discover more of the world around it, or to rather apply what it already knows and exploit this knowledge to maximise the expected return. There is a trade-off since exploiting what we already know will likely lead to some amount of reward, but with imperfect information about the world around the agent there is a possibility that the agent is missing out on some large reward it does not yet know about. There is thus a problem of ensuring good exploration of the state-space while also ensuring at some point we apply what we have learned to ensure good reward. This problem becomes even harder when the environments dynamics are themselves a function of time, and so what we have learned in previous time-steps may become invalid as we progress. This is an active area of research and some possible solutions are presented and discussed in the context of model-based reinforcement learning in later sections.
Multi-armed bandit problems consist of of choosing among multiple discrete arms, each yielding some specific reward with some unknown probability. The common example is that of a slot machine. The reward function of the bandit is unknown, so an agent must interact with it to learn and approximate its reward function. At each point it must make the decision of whether to learn more about the machine or to exploit the knowledge it has gained. Three such strategies for how an agent can decide on an action are now discussed.
\( \epsilon \)-greedy
Epsilon-greedy methods are the simplest methods for deciding on an action with some trade-off between exploring and exploiting. A greedy method is one in which the agent always, greedily, chooses the actions it believes will yield the highest reward. \( \epsilon \)-greedy methods extend this idea to incorporate some non-greedy (exploratory) decisions with some probability \( 1-\epsilon \). In practice these methods are surprisingly robust and performant, and show up in state-of-the-art methods. Some problems with \( \epsilon \)-greedy methods is that it chooses the action to explore indiscriminately. That is, there is no weighting or rule for how to choose what action to explore. The exploration strategy itself may be poor in scenarios where random exploration is not ideal. In practice \( \epsilon=0.99 \) often performs well. Decaying epsilon values are further simple modification which allows an agent to exploits more of its knowledge over time as it gains knowledge and it has explored more of the state space.
Upper Confidence Bound
One of the problems with \( \epsilon \)-greedy strategies was the indiscriminate choice of actions when exploring. One approach is to maintain some prior distribution encoding what we know about the reward function for each state-action pair. This Bayesian strategy allows us to explore possibilities which have high uncertainty in our knowledge - ones which may have high reward. UCB says we should choose the action in which the associated expected reward plus one standard deviation (from our prior of that option) is the highest. Formally, \( \mu+\beta\sigma \) is the upper confidence bound where \( \beta \) is a trade-off parameter which shrinks over time.
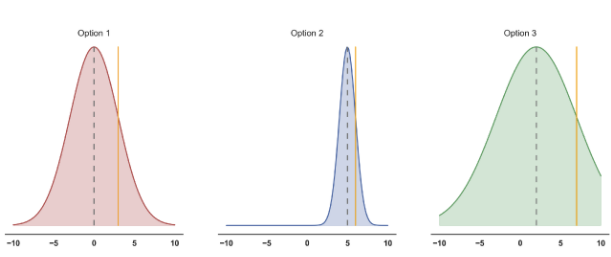
Thompson Sampling
The last strategy to be discussed is that of Thompson sampling - a method which is theoretically similar to UCB. In Thompson sampling we ‘draw’ from each of our prior distributions and order the the resulting rewards. The option which yields the highest reward is selected for exploration. This has the effect that options with high mean rewards \( \mu \) are selected more often, but uncertain events can also be selected since there is large variance in the prior distribution. This method, in contrast to UCB, never gives up on any option. Rather, as we become more certain about the reward priors, choosing options with smaller expected rewards becomes less likely.
References \& Resources
Watch the lecture by David Silver on the trade-offs between exploration and exploitation in the context of reinforcement learning.
 St John
St John 
