What’s the first thing a statistician will say when you dare say the word cause? If you’ve ever taken a statistics class, I have little doubt it was the classic anachronism, Correlation does not imply causation. The classic anachronism seems to imply that we can never state that A causes B from analysis of data. R.A. Fisher, one of the fathers of modern statistics, was stringently opposed to any causal conclusions. But is statistics really powerless when faced with the battle of determining causation? This is exactly what Judea Pearl addresses and calls the causal revolution in his latest book The Book of Why.

In this series of posts I will introduce the mathematical notion of causality from the perspective of statistics in the context of machine learning and artificial intelligence. With the rise in popularity of unsupervised methods in both machine learning and reinforcement learning paradigms, I predict causal inference will play a crucial role in getting our artificial agents to make informed decisions, especially in an uncertain world.
This Series
- A Causal Perspective
- Causal Models
- Learning Causal Models
- Causality and Machine Learning
- Interventions and Multivariate SCMs
- Reaching Rung 3: Counterfactual Reasoning
- Faithfulness
- The Do Calculus
Background
As you probably recall from high school, probability and statistics is almost entirely formulated on the idea or random samples from an experiment. We imagine we are observing possible outcomes from some population of possibilities when drawing from an assortment of independent and identically distributed events. In reality, this assumption of i.i.d. events fails in many situations. Consider shifting some distribution of events or intervening in the system. This is a fundamental basis for the causal approach we shall develop.
In probability theory and statistics, we try to predict an outcome and associate some probability of an event occurring given some distribution of the underlying space of events. In statistical learning, including machine learning, we are performing the inverse problem. We are trying to find the underlying description of the data. The likelihood approach for inference is common in statistics. Machine learning is often a simple extension of this approach - applying knowledge of collected data to infer the underlying structure or pattern of the data generating process.
The causal inference and causal learning problem is a harder one. Even if we had perfect and complete knowledge of the observational distribution, we would still not know the underlying causal structure of the data.
Causal modelling is more fundamental than the probabilistic approach since additional information is contained in such a model. Causal reasoning allows us to analyze the effects of interventions or distribution changes and make predictions in a more general sense than conventional statistical approaches. Inferring causal structure thus becomes the inverse problem. Using observational data and outcomes, as well as intervention data, we would like to infer the underlying relationships between the appropriate variables of interest.
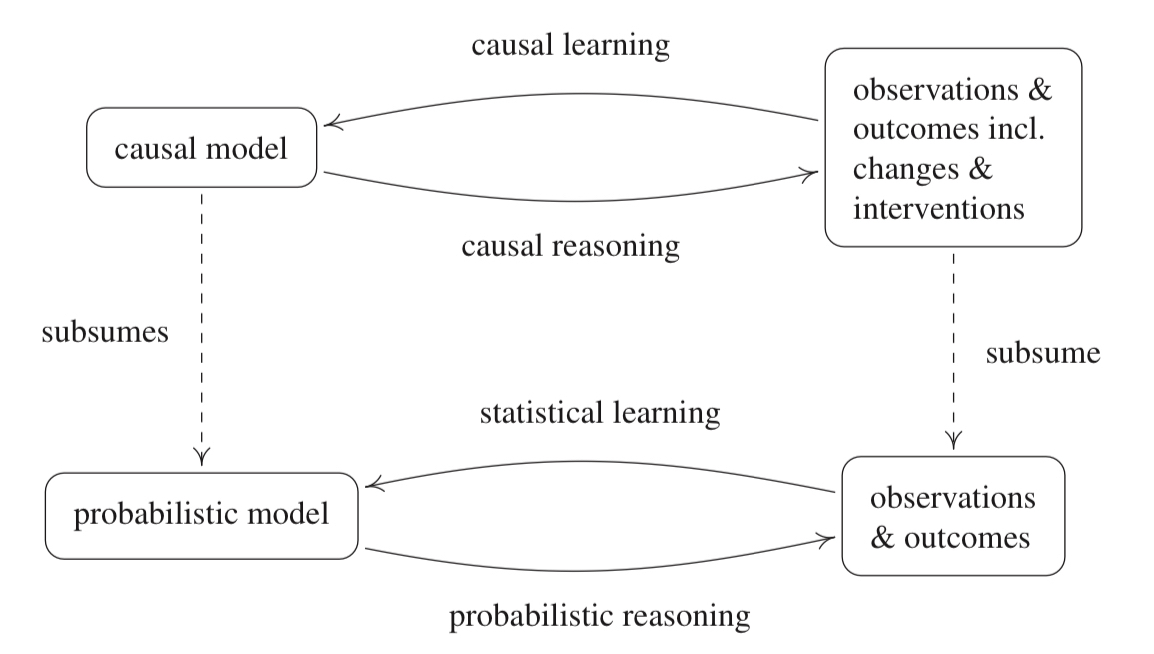
Although we cannot infer concrete causal structure, we can at least infer the existence of the underlying causal connections from statistical dependence between them. Let’s begin!
Theory
Reichenbach’s common cause principle: Given two statistically dependent random variables \(X\) and \(Y\), there exists a third variable \(Z\) that causally influences both \(X\) and \(Y\) - a common cause. A special case is, of course, the situation when \(Z\) is \(X\) or \(Y\). Also, this common cause ‘shields’ the two variables from each other. Formally, given \(Z\), \(X\) is independent of \(Y\).

At this point we can realise there is a very important difference between conditioning on a variable and intervening. By conditioning we are ‘asking’ our data what we observe when one variable has a certain value. When intervening, however, we are changing a variable and seeing how the system responds. This is where modelling dependencies becomes crucial.
Structural Causal Models Jonas Peters introduces SCMs using the classic problem in machine learning of recognising and classifying handwritten digits - usually done using the MNIST dataset. Let us consider how this data was collected. Let’s say in scenario (i) we tell someone the number to write. In other words, we give them the ‘label’ and they write the corresponding number. In scenario (ii), the person decided the number to write and gives the digit an associated label. The resulting dataset will look exactly the same, and so the joint density distribution will be exactly the same. However, we know there is a fundamental difference. Calling the label \(Y\) and the handwritten digit \(X\), if we intervene on \(Y\) by changing the label, the result will be a different handwritten digit since the label we ‘give’ causes the resulting handwritten digit. In scenario (ii), changing the label does not change the handwritten digit. There is a common cause - the intention of the person writing - but Y does not cause X.
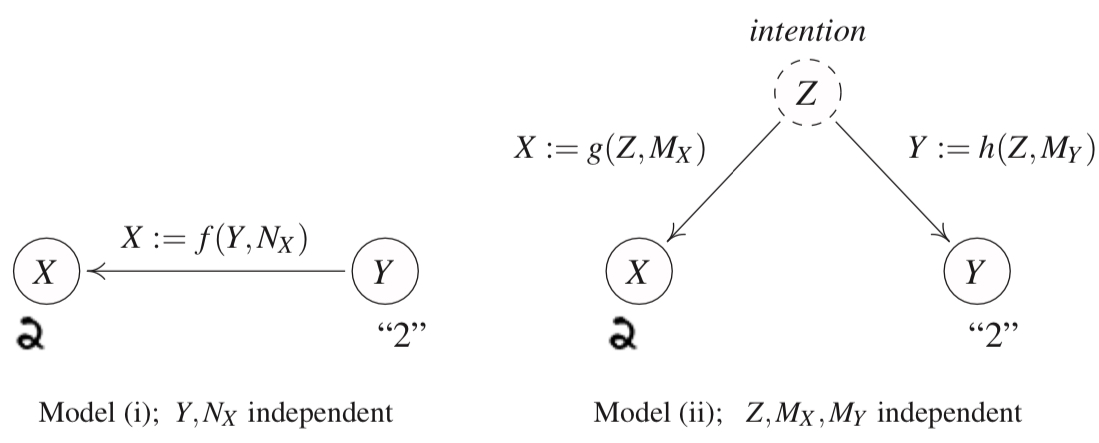
We can thus see that the information contained in the joint distribution over the events is not sufficient to describe the underlying causal structure. SCMs do contain this information and are thus treated as the basis for further theory.
Assumptions for Causal Inference
We are now ready to talk about the basic assumptions needed to develop the modern theory of causal inference. Assumptions of independence are particularly important, so we will spend some time thinking about this. If \(X \rightarrow Y\) is some causal structure, then:
-
It is possible to intervene locally on the variable \(X\) without changing \(Y\). This is the notion of independence we informally discussed previously.
-
Conditioning on a common cause leads to independence. In this scenario, \( p(x) \) and \( p(y|x) \) are autonomous, modular or invariant quantities.
Principle of Independent Mechanisms The causal generative process of system’s variables is composed of autonomous modules that do not inform or influence each other.
This principle makes sense if we think of these modules as being physical mechanisms in the real world. The idea is that if we intervene by changing one mechanism, the other will be unaffected. This assumption can help with the idea of transferring knowledge between related domains. How different is a robot serving ice cream from an industrial robot moving car parts?
Crucially, all this is to say that the mechanism generating the effect from its cause contains no information about the mechanism generating the cause.
The Physics of Causality
To end off this part of the causality series, I’ll briefly discuss some of the connections to physics and the real world in more depth. The readers less motivated by the physics can ignore this without worry!
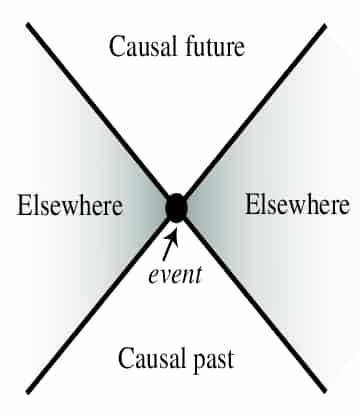
The theory of relativity tells us that an events can only influence other events that fall in its light cone. Many would argue that time should be invertible - at least on the small scale. This issue is resolved by considering a complexity measure for the states. In a thermodynamic and information theoretic way, we can think of the entropy increasing as time moves forward. This can prohibit the invertibility of the system even if the directions of time are otherwise indistinguishable.
Next up
In this article we motivated and formulate some ideas for modern theories of causal inference. In the next ‘episode’ of this series we shall develop the mathematics which becomes crucial when dealing with larger models. These are the structural causal models we briefly introduced.
 St John
St John